Skip to content

00. Prefix Sum & Line Swipe

Prefix Sum

Theory

Description

The prefix sum technique allows for efficient range sum queries by precomputing cumulative sums in an array.

Steps

  1. Build the Prefix Sum Array:
    Create a new array prefix where each element at index i stores the sum of elements from the start of the array up to index i:

    prefix[0] = arr[0]
prefix[1] = arr[0] + arr[1]
prefix[2] = arr[0] + arr[1] + arr[2]
    And so on…
    Example:
    For arr = [3, 1, 4, 1, 5, 9], the prefix_sum array is [3, 4, 8, 9, 14, 23].

  2. Answer Range Sum Queries:
    To find the sum of elements between indices i and j, use:
    sum(i, j) = prefix[j] - prefix[i-1]
    Example:
    For arr = [3, 1, 4, 1, 5, 9], the sum from index 2 to 4:
    sum(2, 4) = prefix[4] - prefix[1] = 14 - 4 = 10.

Note

If i = 0, simply return prefix[j].

Time & Space Complexity

  • Time: O(n) for building the prefix sum array, O(1) per query.
  • Space: O(n) for storing the prefix sum array.

Problems

1. Range Sum Query - Immutable (Leetcode:303)

Problem Statement

Given an integer array nums, handle multiple queries of the following type:

Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Implement the NumArray class:

  • NumArray(int[] nums) Initializes the object with the integer array nums.
  • int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

Example 1:

Input
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
Output
[null, 1, -1, -3]

Explanation
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3

Constraints:

  • 1 <= nums.length <= 104
  • -105 <= nums[i] <= 105
  • 0 <= left <= right < nums.length
  • At most 104 calls will be made to sumRange.
Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
class NumArray:

def __init__(self, nums: List[int]):
    self.prefix_sum = [0] * (len(nums)+1)

    for i in range(len(nums)):
        self.prefix_sum[i+1] = self.prefix_sum[i] + nums[i]

def sumRange(self, left: int, right: int) -> int:
    return self.prefix_sum[right+1]-self.prefix_sum[left]
Explaination

  1. Constructor (__init__):

    • Initializes a list prefix_sum where prefix_sum[i] stores the sum of the elements from index 0 to i-1.
    • Builds this prefix_sum array by iterating over the input list nums.

  2. Method sumRange(left, right) :

    • Returns the sum of the subarray between indices left and right by calculating the difference:
      prefix_sum[right+1] - prefix_sum[left].
    • This allows constant time O(1) querying of subarray sums after the initial setup.

2. Left and Right Sum Differences (Leetcode:2574)

Problem Statement

Given a 0-indexed integer array nums, find a 0-indexed integer array answer where:

  • answer.length == nums.length.
  • answer[i] = |leftSum[i] - rightSum[i]|.

Where:

  • leftSum[i] is the sum of elements to the left of the index i in the array nums. If there is no such element, leftSum[i] = 0.
  • rightSum[i] is the sum of elements to the right of the index i in the array nums. If there is no such element, rightSum[i] = 0.
    Return the array answer.

Example 1:

Input: nums = [10,4,8,3]
Output: [15,1,11,22]
Explanation: The array leftSum is [0,10,14,22] and the array rightSum is [15,11,3,0].
The array answer is [|0 - 15|,|10 - 11|,|14 - 3|,|22 - 0|] = [15,1,11,22].

Example 2:

Input: nums = [1]
Output: [0]
Explanation: The array leftSum is [0] and the array rightSum is [0].
The array answer is [|0 - 0|] = [0].

Constraints:

  • 1 <= nums.length <= 1000
  • 1 <= nums[i] <= 105
code & Explanation 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
def leftRightDifference(self, nums: List[int]) -> List[int]:

    left_sum  = 0
    right_sum = sum(nums)
    answer = []

    for num in nums:
        left_sum += num
        answer.append(abs(left_sum-right_sum))
        right_sum -= num

    return answer
Explaination

  1. Initialization :

    • left_sum = 0: Tracks the sum of elements before the current index.
    • right_sum = sum(nums): Initially holds the total sum of all elements.
    • answer = []: Stores the result.

  2. Loop through nums :

    • For each element num:
    • Update left_sum: Add num to left_sum.
    • Calculate and append absolute difference: |left_sum - right_sum| is appended to answer.
    • Update right_sum: Subtract num from right_sum.

  3. Return answer :

    • After the loop, return the computed differences in answer.

3. XOR Queries of a Subarray (Leetcode:1310)

Problem Statement

You are given an array arr of positive integers. You are also given the array queries where queries[i] = [lefti, righti].

For each query i compute the XOR of elements from lefti to righti (that is, arr[lefti] XOR arr[lefti + 1] XOR ... XOR arr[righti] ).

Return an array answer where answer[i] is the answer to the ith query.

Example 1:

Input: arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
Output: [2,7,14,8]
Explanation: The binary representation of the elements in the array are:
1 = 0001
3 = 0011
4 = 0100
8 = 1000
The XOR values for queries are:
[0,1] = 1 xor 3 = 2
[1,2] = 3 xor 4 = 7
[0,3] = 1 xor 3 xor 4 xor 8 = 14
[3,3] = 8```

Example 2:

Input: arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]]
Output: [8,0,4,4]

Constraints:

  • 1 <= arr.length, queries.length <= 3 * 104
  • 1 <= arr[i] <= 109
  • queries[i].length == 2
  • 0 <= lefti <= righti < arr.length
Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def xorQueries(self, arr: List[int], queries: List[List[int]]) -> List[int]:

        prefix = [0] * (len(arr) + 1)
        answer = []

        for i in range(len(arr)):
            prefix[i + 1] = prefix[i] ^ arr[i]

        for left, right in queries:
            answer.append(prefix[right + 1] ^ prefix[left])

        return answer
Explaination:

  1. Initialization:

    • prefix = [0] * (len(arr) + 1): Create a list prefix to store the cumulative XOR of elements in the array. The extra element accounts for the starting point (index 0).
    • answer = []: This will store the result for each query.

  2. Build Prefix XOR Array:

    • For each element arr[i] in the array, compute the cumulative XOR up to that index:
    • prefix[i + 1] = prefix[i] ^ arr[i]: This updates the prefix list, where each entry at i + 1 holds the XOR of all elements from the start of the array up to index i.

  3. Process Queries:

    • For each query [left, right], calculate the XOR of elements from index left to right:
    • answer.append(prefix[right + 1] ^ prefix[left]): This uses the precomputed prefix array. The XOR of the subarray from left to right is found by subtracting the prefix XORs at left and right + 1.

  4. Return the Answer:

    • The final answer list contains the result for each query, which is the XOR of the elements in the subarray defined by left and right.

4. Subarray Sum Equals K (Leetcode:560)

Problem Statement

Given an array of integers nums and an integer k, return the total number of subarrays whose sum equals to k.

A subarray is a contiguous non-empty sequence of elements within an array.

Example 1:

Input: nums = [1,1,1], k = 2
Output: 2

Example 2:

Input: nums = [1,2,3], k = 3
Output: 2

Constraints:

  • 1 <= nums.length <= 2 * 104
  • -1000 <= nums[i] <= 1000
  • -107 <= k <= 107
Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        count = 0
        prefix_sum = 0
        dictionary = {0:1}  # Start with {0:1} to handle subarrays starting from the beginning

        for num in nums:
            prefix_sum += num  # Update prefix sum
            diff = prefix_sum - k  # Find the difference between the current prefix sum and target k
            if diff in dictionary:  # If this diff has been seen before, increment count
                count += dictionary[diff]
            dictionary[prefix_sum] = dictionary.get(prefix_sum, 0) + 1  # Update the dictionary

        return count
Explaination:

  1. Initialization:

    • count = 0: To store the number of valid subarrays.
    • prefix_sum = 0: To keep track of the cumulative sum as we iterate through the array.
    • dictionary = {0: 1}: This keeps track of how many times a certain prefix sum has occurred.
    • We start with {0: 1} because a sum of 0 is possible before we start processing the array.

  2. Iterate through the array:

    • For each element num in the array, update the prefix_sum by adding num to it.
    • Compute the difference diff = prefix_sum - k. If diff exists in the dictionary, it means there are subarrays whose sum equals k, and their count is stored in the dictionary.
    • Increment count by the number of times diff has occurred.
    • Update the dictionary by increasing the count of prefix_sum.

  3. Return the count:

    • This gives the total number of subarrays whose sum equals k.

5. Product of Array Except Self (Leetcode:238)

Problem Statement

Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].

The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.

You must write an algorithm that runs in O(n) time and without using the division operation.

Example 1:

Input: nums = [1,2,3,4]
Output: [24,12,8,6]

Example 2:

Input: nums = [-1,1,0,-3,3]
Output: [0,0,9,0,0]

Constraints:

2 <= nums.length <= 10^5
-30 <= nums[i] <= 30
The input is generated such that answer[i] is guaranteed to fit in a 32-bit integer.

Follow up:

Can you solve the problem in O(1) extra space complexity? (The output array does not count as extra space for space complexity analysis.)

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
def productExceptSelf(self, nums: List[int]) -> List[int]:
    n = len(nums)
    answer = [1] * n

    prefix = 1
    for i in range(n):
        answer[i] = prefix
        prefix *= nums[i]

    suffix = 1
    for i in range(n - 1, -1, -1):
        answer[i] *= suffix
        suffix *= nums[i]

    return answer
Explaination:
This is first approach

6. Increment Submatrices by One (Leetcode:2536)

Problem Statement

You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.

You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:

Add 1 to every element in the submatrix with the top left corner (row1i, col1i) and the bottom right corner (row2i, col2i). That is, add 1 to mat[x][y] for all row1i <= x <= row2i and col1i <= y <= col2i.

Return the matrix mat after performing every query.

Example 1:

Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Example 2:

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.

Constraints:

1 <= n <= 500
1 <= queries.length <= 10^4
0 <= row1i <= row2i < n
0 <= col1i <= col2i < n

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
def rangeAddQueries(self, n: int, queries: List[List[int]]) -> List[List[int]]:
    diff = [[0] * (n + 1) for _ in range(n + 1)]

    for r1, c1, r2, c2 in queries:
        diff[r1][c1] += 1
        if c2 + 1 < n:
            diff[r1][c2 + 1] -= 1
        if r2 + 1 < n:
            diff[r2 + 1][c1] -= 1
        if r2 + 1 < n and c2 + 1 < n:
            diff[r2 + 1][c2 + 1] += 1

    mat = [[0] * n for _ in range(n)]
    for i in range(n):
        for j in range(n):
            top = mat[i-1][j] if i > 0 else 0
            left = mat[i][j-1] if j > 0 else 0
            corner = mat[i-1][j-1] if i > 0 and j > 0 else 0
            mat[i][j] = diff[i][j] + top + left - corner

    return mat
Explaination:
This is first approach

7. Range Sum Query 2D - Immutable (Leetcode:304)

Problem Statement

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:
NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

Input:
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output:
[null, 8, 11, 12]
Explanation:
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10^4 <= matrix[i][j] <= 10^4
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10^4 calls will be made to sumRegion.

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class NumMatrix:
    def __init__(self, matrix: List[List[int]]):

        if not matrix or not matrix[0]:
            return

        m, n = len(matrix), len(matrix[0])
        # Create prefix sum matrix with an extra row and column
        self.prefixSum = [[0] * (n + 1) for _ in range(m + 1)]

        # Compute prefix sums
        for i in range(m):
            for j in range(n):
                self.prefixSum[i+1][j+1] = (
                    matrix[i][j]
                    + self.prefixSum[i][j+1]
                    + self.prefixSum[i+1][j]
                    - self.prefixSum[i][j]
                )

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return (
            self.prefixSum[row2+1][col2+1]
            - self.prefixSum[row1][col2+1]
            - self.prefixSum[row2+1][col1]
            + self.prefixSum[row1][col1]
        )


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)
Explaination:
This is first approach

8. Power of Heroes (Leetcode:2681)

Problem Statement

You are given a 0-indexed integer array nums representing the strength of some heroes. The power of a group of heroes is defined as follows:

Let i0, i1, ... ,ik be the indices of the heroes in a group. Then, the power of this group is max(nums[i0], nums[i1], ... ,nums[ik])2 * min(nums[i0], nums[i1], ... ,nums[ik]).

Return the sum of the power of all non-empty groups of heroes possible. Since the sum could be very large, return it modulo 10^9 + 7.

Example 1:

Input: nums = [2,1,4]
Output: 141
Explanation:
1st group: [2] has power = 22 * 2 = 8.
2nd group: [1] has power = 12 * 1 = 1.
3rd group: [4] has power = 42 * 4 = 64.
4th group: [2,1] has power = 22 * 1 = 4.
5th group: [2,4] has power = 42 * 2 = 32.
6th group: [1,4] has power = 42 * 1 = 16.
​​​​​​​7th group: [2,1,4] has power = 42​​​​​​​ * 1 = 16.
The sum of powers of all groups is 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141.

Example 2:

Input: nums = [1,1,1]
Output: 7
Explanation: A total of 7 groups are possible, and the power of each group will be 1. Therefore, the sum of the powers of all groups is 7.

Constraints:

1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def sumOfPower(self, nums: List[int]) -> int:
    MOD = 10**9 + 7
    nums.sort()
    res = 0
    prefixSum = 0

    for x in nums:
        contribution = (x * x % MOD) * ((x + prefixSum) % MOD) % MOD
        res = (res + contribution) % MOD
        prefixSum = (prefixSum * 2 + x) % MOD

    return res
Explaination:
This is first approach

9. Minimum Cost to Make Array Equal (Leetcode:2448)

Problem Statement

You are given two 0-indexed arrays nums and cost consisting each of n positive integers.

You can do the following operation any number of times:

  • Increase or decrease any element of the array nums by 1.

The cost of doing one operation on the i^th element is cost[i].

Return the minimum total cost such that all the elements of the array nums become equal.

Example 1:

Input: nums = [1,3,5,2], cost = [2,3,1,14]
Output: 8
Explanation: We can make all the elements equal to 2 in the following way:
- Increase the 0th element one time. The cost is 2.
- Decrease the 1st element one time. The cost is 3.
- Decrease the 2nd element three times. The cost is 1 + 1 + 1 = 3.
The total cost is 2 + 3 + 3 = 8.
It can be shown that we cannot make the array equal with a smaller cost.

Example 2:

Input: nums = [2,2,2,2,2], cost = [4,2,8,1,3]
Output: 0
Explanation: All the elements are already equal, so no operations are needed.

Constraints:

n == nums.length == cost.length
1 <= n <= 10^5
1 <= nums[i], cost[i] <= 10^6
Test cases are generated in a way that the output doesn't exceed 2^53-1

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
def minCost(self, nums: List[int], cost: List[int]) -> int:
    pairs = sorted(zip(nums, cost))
    total_cost = sum(cost)

    # Step 2: Find weighted median
    acc = 0
    for num, c in pairs:
        acc += c
        if acc >= (total_cost + 1) // 2:  # ceil(total_cost / 2)
            target = num
            break

    # Step 3: Compute total cost to convert all nums to target
    res = 0
    for num, c in pairs:
        res += abs(num - target) * c

    return res
Explaination:
This is first approach

Line Sweep

Theory

Description

The Line Sweep Algorithm is a powerful technique used in computational geometry. It's an efficient way to solve problems like detecting intersections, finding the closest pair of points, or calculating the convex hull. Let’s break down the core concepts of this algorithm to understand how it works.

What is the Sweep Line?

The sweep line is an imaginary vertical line that moves across a plane from left to right. As it moves, it sweeps through the objects in its path, processing important events at each step. Imagine it like a curtain slowly moving across a stage, revealing different parts of a scene. In the context of algorithms, this "curtain" moves across the plane, checking and reacting to specific points where events occur.

The sweep line doesn’t just move randomly—it advances through key points, called events, which are defined based on the specific problem being solved. By focusing on these events, the algorithm can efficiently process only the relevant parts of the data.

What are Events?

An event is a point on the plane where something significant happens as the sweep line moves. These events are the heart of the algorithm because they trigger actions like adding or removing objects, or checking for interactions. Depending on the problem you're solving, events could include:

  • Start events: The beginning of an object, such as the left endpoint of a line segment or the opening of a rectangle.
  • End events: The end of an object, like the right endpoint of a line segment or the closing of a rectangle.
  • Intersection events: When two objects, like two line segments, intersect or overlap.

The sweep line processes these events in order, one by one, and each event may lead to an update in the algorithm’s state—whether it’s adding a new object, removing one, or checking for an intersection.

How Does it Work?

Here’s how the line sweep algorithm works in practice:

  • Sort the events: The first step is to sort all the events in order of their position along the x-axis (left to right). For example, if you are working with line segments, this would mean sorting by the x-coordinate of the start and end points of each segment.

  • Process events in order: The sweep line starts at the leftmost event and moves to the right. For each event, you do something specific:

  • When the sweep line reaches a start event (like the left endpoint of a line segment), the segment is added to a list of active objects.
  • When the sweep line reaches an end event (like the right endpoint), that segment is removed from the list of active objects.
  • At each step, the algorithm may check for intersections or other interactions between active objects (e.g., checking if newly added segments intersect with others already in the list).

By sorting and processing events in this way, the algorithm can handle complex geometric problems without having to check every possible pair of objects, which would be much slower.

Problems

1. Points That Intersect With Cars (Leetcode:2848)

Problem Statement

You are given a 0-indexed 2D integer array nums representing the coordinates of the cars parking on a number line.
For any index i, nums[i] = [starti, endi] where starti is the starting point of the ith car and endi is the ending point of the ith car.

Return the number of integer points on the line that are covered with any part of a car.

Example 1:

Input: nums = [[3,6],[1,5],[4,7]]
Output: 7
Explanation: All the points from 1 to 7 intersect at least one car, therefore the answer would be 7.

Example 2:

Input: nums = [[1,3],[5,8]]
Output: 7
Explanation: Points intersecting at least one car are 1, 2, 3, 5, 6, 7, 8. There are a total of 7 points, therefore the answer would be 7.

Constraints:

1 <= nums.length <= 100
nums[i].length == 2
1 <= starti <= endi <= 100

Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def numberOfPoints(self, nums: List[List[int]]) -> int:

        line = [0] * 102
        points_on_line = 0

        for start,end in nums:
            line[start] += 1
            line[end + 1] -= 1

        for i in range(1, 102):
            line[i] += line[i - 1]
            if line[i] != 0:
                points_on_line += 1

        return points_on_line
Explaination:

2. Check if All the Integers in a Range Are Covered (Leetcode:1893)

Problem Statement

You are given a 2D integer array ranges and two integers left and right. Each ranges[i] = [starti, endi]represents an inclusive interval between starti and endi.

Return true if each integer in the inclusive range [left, right] is covered by at least one interval in ranges. Return false otherwise.

An integer x is covered by an interval ranges[i] = [starti, endi] if starti <= x <= endi.

Example 1:

Input: ranges = [[1,2],[3,4],[5,6]], left = 2, right = 5
Output: true
Explanation: Every integer between 2 and 5 is covered:
- 2 is covered by the first range.
- 3 and 4 are covered by the second range.
- 5 is covered by the third range.

Example 2:

Input: ranges = [[1,10],[10,20]], left = 21, right = 21
Output: false
Explanation: 21 is not covered by any range.

Constraints:

1 <= ranges.length <= 50
1 <= starti <= endi <= 50
1 <= left <= right <= 50

Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def isCovered(self, ranges: List[List[int]], left: int, right: int) -> bool:
        line = [0] * 52

        for start,end in ranges:
            line[start]+=1
            line[end+1]-=1

        for i in range(1, 52):
            line[i] += line[i - 1]

        for i in range(left, right+1):
            if line[i]<1:
                return False

        return True
Explaination:

3. Minimum Number of Arrows to Burst Balloons (Leetcode:452)

Problem Statement

There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.

Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.

Given the array points, return the minimum number of arrows that must be shot to burst all balloons.

Example 1:

Input: points = [[10,16],[2,8],[1,6],[7,12]]
Output: 2
Explanation: The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons [2,8] and [1,6].
- Shoot an arrow at x = 11, bursting the balloons [10,16] and [7,12].

Example 2:

Input: points = [[1,2],[3,4],[5,6],[7,8]]
Output: 4
Explanation: One arrow needs to be shot for each balloon for a total of 4 arrows.

Example 3:

Input: points = [[1,2],[2,3],[3,4],[4,5]]
Output: 2
Explanation: The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 2, bursting the balloons [1,2] and [2,3].
- Shoot an arrow at x = 4, bursting the balloons [3,4] and [4,5].

Constraints:

1 <= points.length <= 10^5
points[i].length == 2
-2^31 <= xstart < xend <= 2^31 - 1

Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        prev = points[0][1]
        arrows = 1

        for start, end in sorted(points)[1:]:
            if start>prev :
                prev = end
                arrows+=1

            prev = min(end, prev)
        return arrows
Explaination:

4.Car Pooling (Leetcode:1094)

Problem Statement

There is a car with capacity empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).

You are given the integer capacity and an array trips where trips[i] = [numPassengersi, fromi, toi] indicates that the ith trip has numPassengersi passengers and the locations to pick them up and drop them off are fromi and toi respectively. The locations are given as the number of kilometers due east from the car's initial location.

Return true if it is possible to pick up and drop off all passengers for all the given trips, or false otherwise.

Example 1:

Input: trips = [[2,1,5],[3,3,7]], capacity = 4
Output: false
Example 2:

Example 2:

Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: true

Constraints:

1 <= trips.length <= 1000
trips[i].length == 3
1 <= numPassengersi <= 100
0 <= fromi < toi <= 1000
1 <= capacity <= 10^5

Code & Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution(object):
    def carPooling(self, trips: List[List[int]], capacity: int) -> bool:
        locations = [0] * 1001
        for numPassengers, start, end in trips:
            locations[start] += numPassengers
            locations[end] -= numPassengers

        for numPassengers in locations:
            capacity -= numPassengers
            if capacity < 0: 
                return False

        return True
Explaination:

5. My Calendar II (Leetcode:731)

Problem Statement

You are implementing a program to use as your calendar. We can add a new event if adding the event will not cause a triple booking.

A triple booking happens when three events have some non-empty intersection (i.e., some moment is common to all the three events.).

The event can be represented as a pair of integers startTime and endTime that represents a booking on the half-open interval [startTime, endTime), the range of real numbers x such that startTime <= x < endTime.

Implement the MyCalendarTwo class:

  • MyCalendarTwo() Initializes the calendar object.
  • boolean book(int startTime, int endTime) Returns true if the event can be added to the calendar successfully without causing a triple booking. Otherwise, return false and do not add the event to the calendar.

Example 1:

Input:
["MyCalendarTwo", "book", "book", "book", "book", "book", "book"]
[[], [10, 20], [50, 60], [10, 40], [5, 15], [5, 10], [25, 55]]
Output:
[null, true, true, true, false, true, true]
>Explanation:
MyCalendarTwo myCalendarTwo = new MyCalendarTwo();
myCalendarTwo.book(10, 20); // return True, The event can be booked.
myCalendarTwo.book(50, 60); // return True, The event can be booked.
myCalendarTwo.book(10, 40); // return True, The event can be double booked.
myCalendarTwo.book(5, 15); // return False, The event cannot be booked, because it would result in a triple booking. myCalendarTwo.book(5, 10); // return True, The event can be booked, as it does not use time 10 which is already double booked.
myCalendarTwo.book(25, 55); // return True, The event can be booked, as the time in [25, 40) will be double booked with the third event, the time [40, 50) will be single booked, and the time [50, 55) will be double booked with the second event.

Constraints:

0 <= start < end <= 109
At most 1000 calls will be made to book.

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class MyCalendarTwo:

    def __init__(self):
        self.bookings = []
        self.overlaps = []

    def book(self, startTime: int, endTime: int) -> bool:
        # Step 1: Check if overlaps with any double booking (would cause triple booking)
        for o_start, o_end in self.overlaps:
            if max(startTime, o_start) < min(endTime, o_end):
                return False  # Triple booking would occur

        # Step 2: Record new double bookings caused by this event
        for b_start, b_end in self.bookings:
            if max(startTime, b_start) < min(endTime, b_end):  # They overlap
                overlap_start = max(startTime, b_start)
                overlap_end = min(endTime, b_end)
                self.overlaps.append((overlap_start, overlap_end))

        # Step 3: Record this booking
        self.bookings.append((startTime, endTime))
        return True

# Your MyCalendarTwo object will be instantiated and called as such:
# obj = MyCalendarTwo()
# param_1 = obj.book(startTime,endTime)
Explaination:
This is first approach

6. Number of Flowers in Full Bloom (Leetcode:2251)

Problem Statement

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [starti, endi] means the ith flower will be in full bloom from starti to endi (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the ith person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the ith person arrives.

Example 1:
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10^4
flowers[i].length == 2
1 <= starti <= endi <= 10^9
1 <= people.length <= 5 * 10^4
1 <= people[i] <= 10^9

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:

    events: List[Tuple[int, int, int]] = []

    # Encode flower bloom events
    for start, end in flowers:
        events.append((start, 1, -1))       # +1 bloom starts at start time
        events.append((end + 1, -1, -1))    # -1 bloom ends just after end time

    # Encode people's arrival events
    for idx, arrival_time in enumerate(people):
        events.append((arrival_time, 2, idx))  # 2 = person arrives

    # Sort all events:
    # - First by time
    # - Then by event type: start (1), person (2), end (-1) in that order
    events.sort()

    blooming_flowers = 0
    result = [0] * len(people)

    for time, event_type, idx in events:
        if event_type == 2:  # person arrival
            result[idx] = blooming_flowers
        else:
            blooming_flowers += event_type  # +1 for start, -1 for end

    return result
Explaination:
This is first approach

7. My Calendar III (Leetcode:732)

Problem Statement

A k-booking happens when k events have some non-empty intersection (i.e., there is some time that is common to all k events.)

You are given some events [startTime, endTime), after each given event, return an integer k representing the maximum k-booking between all the previous events.

Implement the MyCalendarThree class:

  • MyCalendarThree() Initializes the object.
  • int book(int startTime, int endTime) Returns an integer k representing the largest integer such that there exists a k-booking in the calendar.

Example 1:

Input
["MyCalendarThree", "book", "book", "book", "book", "book", "book"]
[[], [10, 20], [50, 60], [10, 40], [5, 15], [5, 10], [25, 55]]
Output
[null, 1, 1, 2, 3, 3, 3]
Explanation
MyCalendarThree myCalendarThree = new MyCalendarThree();
myCalendarThree.book(10, 20); // return 1
myCalendarThree.book(50, 60); // return 1
myCalendarThree.book(10, 40); // return 2
myCalendarThree.book(5, 15); // return 3
myCalendarThree.book(5, 10); // return 3
myCalendarThree.book(25, 55); // return 3

Constraints:

0 <= startTime < endTime <= 10^9
At most 400 calls will be made to book.

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class MyCalendarThree:

    def __init__(self):
        self.timeline = defaultdict(int)
        self.max_overlap = 0

    def book(self, startTime: int, endTime: int) -> int:
        self.timeline[startTime] += 1
        self.timeline[endTime] -= 1

        # Sweep line
        ongoing = 0
        for time in sorted(self.timeline):
            ongoing += self.timeline[time]
            self.max_overlap = max(self.max_overlap, ongoing)

        return self.max_overlap

# Your MyCalendarThree object will be instantiated and called as such:
# obj = MyCalendarThree()
# param_1 = obj.book(startTime,endTime)
Explaination:
This is first approach

8. Minimum Number of Taps to Open to Water a Garden (Leetcode:1326)

Problem Statement

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e., the length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

Example 1:

Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

Constraints:

1 <= n <= 104
ranges.length == n + 1
0 <= ranges[i] <= 100

Code and Explaination 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def minTaps(self, n: int, ranges: List[int]) -> int:
    max_reach = [0] * (n + 1)

    # Build max_reach array from ranges
    for i, r in enumerate(ranges):
        left = max(0, i - r)
        right = min(n, i + r)
        max_reach[left] = max(max_reach[left], right)

    # Update max_reach to reflect the farthest reachable position from any point <= i
    for i in range(1, n + 1):
        max_reach[i] = max(max_reach[i], max_reach[i - 1])

    taps_opened = 0
    current_end = 0      # Current coverage end
    next_end = 0         # Next coverage end we can jump to

    i = 0
    while current_end < n:
        # While positions are within current coverage,
        # try to find the farthest reach for the next step
        while i <= current_end and i <= n:
            next_end = max(next_end, max_reach[i])
            i += 1

        # If we can't extend coverage, return -1
        if next_end == current_end:
            return -1

        taps_opened += 1
        current_end = next_end

    return taps_opened
Explaination:
This is first approach

9. Minimum Interval to Include Each Query (Leetcode:1851)

Problem Statement

You are given a 2D integer array intervals, where intervals[i] = [lefti, righti] describes the ith interval starting at lefti and ending at righti (inclusive). The size of an interval is defined as the number of integers it contains, or more formally righti - lefti + 1.

You are also given an integer array queries. The answer to the jth query is the size of the smallest interval i such that lefti <= queries[j] <= righti. If no such interval exists, the answer is -1.

Return an array containing the answers to the queries.

Example 1:

Input: intervals = [[1,4],[2,4],[3,6],[4,4]], queries = [2,3,4,5]
Output: [3,3,1,4]
Explanation: The queries are processed as follows:
- Query = 2: The interval [2,4] is the smallest interval containing 2. The answer is 4 - 2 + 1 = 3.
- Query = 3: The interval [2,4] is the smallest interval containing 3. The answer is 4 - 2 + 1 = 3.
- Query = 4: The interval [4,4] is the smallest interval containing 4. The answer is 4 - 4 + 1 = 1.
- Query = 5: The interval [3,6] is the smallest interval containing 5. The answer is 6 - 3 + 1 = 4.

Example 2:

Input: intervals = [[2,3],[2,5],[1,8],[20,25]], queries = [2,19,5,22]
Output: [2,-1,4,6]
Explanation: The queries are processed as follows:
- Query = 2: The interval [2,3] is the smallest interval containing 2. The answer is 3 - 2 + 1 = 2.
- Query = 19: None of the intervals contain 19. The answer is -1.
- Query = 5: The interval [2,5] is the smallest interval containing 5. The answer is 5 - 2 + 1 = 4.
- Query = 22: The interval [20,25] is the smallest interval containing 22. The answer is 25 - 20 + 1 = 6.

Constraints:

  • 1 <= intervals.length <= 105
  • 1 <= queries.length <= 105
  • intervals[i].length == 2
  • 1 <= lefti <= righti <= 107
  • 1 <= queries[j] <= 107
Code and Explaination 

1
Explaination:
This is first approach

1
Explaination:
This is second approach

10. The Skyline Problem (Leetcode: 218)

Problem Statement

A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

  • lefti is the x coordinate of the left edge of the ith building.
  • righti is the x coordinate of the right edge of the ith building.
  • heighti is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:


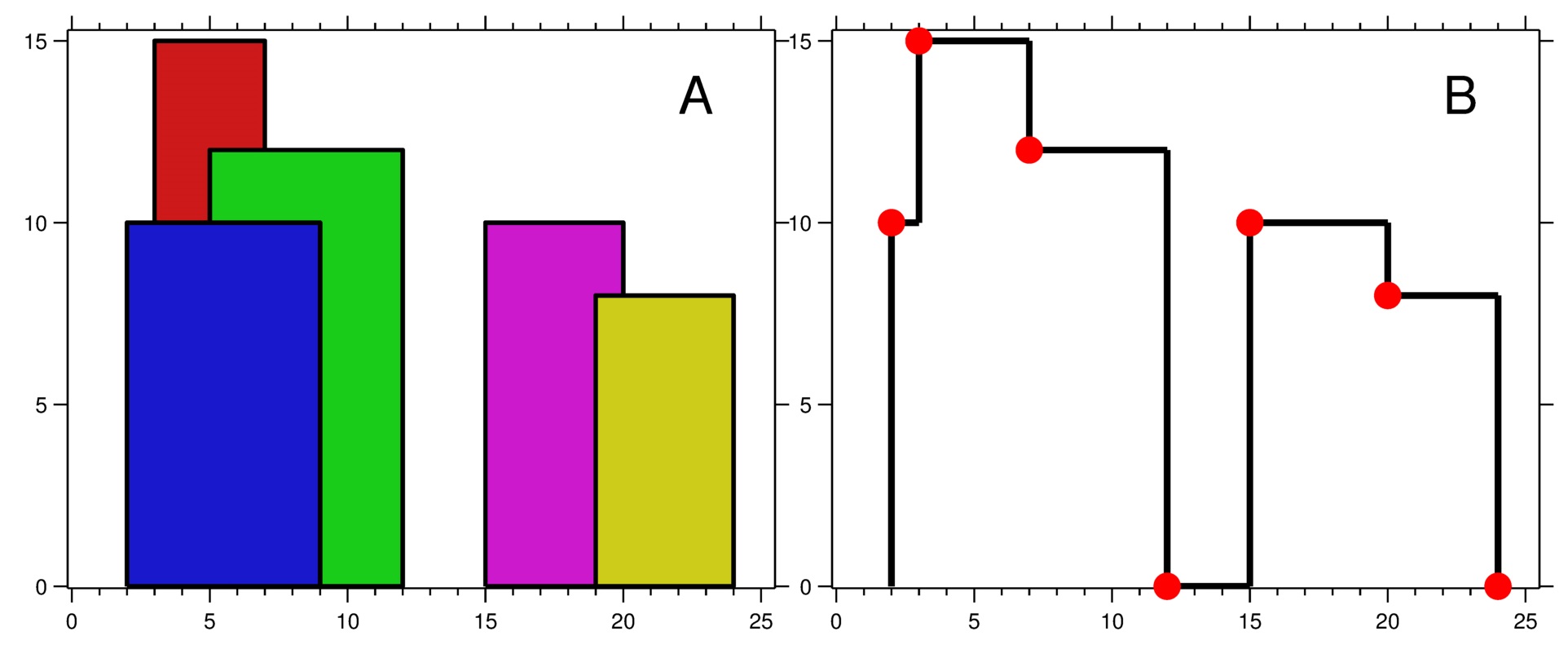
Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:

Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints:

  • 1 <= buildings.length <= 104
  • 0 <= lefti < righti <= 231 - 1
  • 1 <= heighti <= 231 - 1
  • buildings is sorted by lefti in non-decreasing order.
Code and Explaination 

1
Explaination:
This is first approach

1
Explaination:
This is second approach