09. Binary Search
1. Classic Binary Search
Problem 1: Binary Search (Leetcode:704)
Problem Statement
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Example 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1
Constraints:
1 <= nums.length <= 104-104 < nums[i], target < 104- All the integers in
numsare unique.numsis sorted in ascending order.
Problem 2: Search Insert Position (Leetcode:35)
Problem Statement
Given a sorted array of distinct integers and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [1,3,5,6], target = 5
Output: 2
Example 2:
Input: nums = [1,3,5,6], target = 2
Output: 1
Example 3:
Input: nums = [1,3,5,6], target = 7
Output: 4
Constraints:
1 <= nums.length <= 104-104 <= nums[i] <= 104numscontains distinct values sorted in ascending order.-104 <= target <= 104
Problem 3: Peak Index in a Mountain Array (Leetcode:852)
Problem Statement
You are given an integer mountain array arr of length n where the values increase to a peak element and then decrease.
Return the index of the peak element.
Your task is to solve it in O(log(n)) time complexity.
Example 1:
Input: arr = [0,1,0]
Output: 1
Example 2:
Input: arr = [0,2,1,0]
Output: 1
Example 3:
Input: arr = [0,10,5,2]
Output: 1
Constraints:
3 <= arr.length <= 1050 <= arr[i] <= 106arris guaranteed to be a mountain array.
2. First / Last Occurrence
Problem 1: Find First and Last Position of Element in Sorted Array (Leetcode:34)
Problem Statement
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.
If target is not found in the array, return [-1, -1].
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
Example 3:
Input: nums = [], target = 0
Output: [-1,-1]
Constraints:
0 <= nums.length <= 105-109 <= nums[i] <= 109numsis a non-decreasing array.-109 <= target <= 109
Problem 2: Count Occurrences of a Number in a Sorted Array (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
3. Binary Search on Answer (Search Space)
Problem 1: Koko Eating Bananas (Leetcode:875)
Problem Statement
Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.
Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return the minimum integer k such that she can eat all the bananas within h hours.
Example 1:
Input: piles = [3,6,7,11], h = 8
Output: 4
Example 2:
Input: piles = [30,11,23,4,20], h = 5
Output: 30
Example 3:
Input: piles = [30,11,23,4,20], h = 6
Output: 23
Constraints:
1 <= piles.length <= 104piles.length <= h <= 1091 <= piles[i] <= 109
Problem 2: Split Array Largest Sum (Leetcode:410)
Problem Statement
Given an integer array nums and an integer k, split nums into k non-empty subarrays such that the largest sum of any subarray is minimized.
Return the minimized largest sum of the split.
A subarray is a contiguous part of the array.
Example 1:
Input: nums = [7,2,5,10,8], k = 2
Output: 18
Explanation: There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8], where the largest sum among the two subarrays is only 18.
Example 2:
Input: nums = [1,2,3,4,5], k = 2
Output: 9
Explanation: There are four ways to split nums into two subarrays.
The best way is to split it into [1,2,3] and [4,5], where the largest sum among the two subarrays is only 9.
Constraints:
1 <= nums.length <= 10000 <= nums[i] <= 1061 <= k <= min(50, nums.length)
Problem 3: Capacity To Ship Packages Within D Days (Leetcode:1011)
Problem Statement
A conveyor belt has packages that must be shipped from one port to another within days days.
The ith package on the conveyor belt has a weight of weights[i]. Each day, we load the ship with packages on the conveyor belt (in the order given by weights). We may not load more weight than the maximum weight capacity of the ship.
Return the least weight capacity of the ship that will result in all the packages on the conveyor belt being shipped within days days.
Example 1:
Input: weights = [1,2,3,4,5,6,7,8,9,10], days = 5
Output: 15
Explanation: A ship capacity of 15 is the minimum to ship all the packages in 5 days like this:
1st day: 1, 2, 3, 4, 5
2nd day: 6, 7
3rd day: 8
4th day: 9
5th day: 10Note that the cargo must be shipped in the order given, so using a ship of capacity 14 and splitting the packages into parts like (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) is not allowed.
Example 2:
Input: weights = [3,2,2,4,1,4], days = 3
Output: 6
Explanation: A ship capacity of 6 is the minimum to ship all the packages in 3 days like this:
1st day: 3, 2
2nd day: 2, 4
3rd day: 1, 4
Example 3:
Input: weights = [1,2,3,1,1], days = 4
Output: 3
Explanation:
1st day: 1
2nd day: 2
3rd day: 3
4th day: 1, 1
Constraints:
1 <= days <= weights.length <= 5 * 1041 <= weights[i] <= 500
Problem 4: Find the Smallest Divisor Given a Threshold (Leetcode:1283)
Problem Statement
Given an array of integers nums and an integer threshold, we will choose a positive integer divisor, divide all the array by it, and sum the division's result. Find the smallest divisor such that the result mentioned above is less than or equal to threshold.
Each result of the division is rounded to the nearest integer greater than or equal to that element. (For example: 7/3 = 3 and 10/2 = 5).
The test cases are generated so that there will be an answer.
Example 1:
Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1.
If the divisor is 4 we can get a sum of 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).
Example 2:
Input: nums = [44,22,33,11,1], threshold = 5
Output: 44
Constraints:
1 <= nums.length <= 5 * 1041 <= nums[i] <= 106nums.length <= threshold <= 106
4. Binary Search in Rotated Sorted Array
Problem 1: Search in Rotated Sorted Array (Leetcode:33)
Problem Statement
There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is possibly left rotated at an unknown index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be left rotated by 3 indices and become [4,5,6,7,0,1,2].
Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
Example 3:
Input: nums = [1], target = 0
Output: -1
Constraints:
1 <= nums.length <= 5000-104 <= nums[i] <= 104- All values of
numsare unique.numsis an ascending array that is possibly rotated.-104 <= target <= 104
Problem 2: Search in Rotated Sorted Array II (Leetcode:81)
Problem Statement
There is an integer array nums sorted in non-decreasing order (not necessarily with distinct values).
Before being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,4,4,5,6,6,7] might be rotated at pivot index 5 and become [4,5,6,6,7,0,1,2,4,4].
Given the array nums after the rotation and an integer target, return true if target is in nums, or false if it is not in nums.
You must decrease the overall operation steps as much as possible.
Example 1:
Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true
Example 2:
Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false
Constraints:
1 <= nums.length <= 5000-104 <= nums[i] <= 104numsis guaranteed to be rotated at some pivot.-104 <= target <= 104
Follow up: This problem is similar to Search in Rotated Sorted Array, but nums may contain duplicates. Would this affect the runtime complexity? How and why?
5. Lower Bound / Upper Bound
Problem 1: Longest Increasing Subsequence (Leetcode:300)
Problem Statement
Given an integer array nums, return the length of the longest strictly increasing subsequence**.
Example 1:
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Example 2:
Input: nums = [0,1,0,3,2,3]
Output: 4
Example 3:
Input: nums = [7,7,7,7,7,7,7]
Output: 1
Constraints:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?
Problem 2: Find Peak Element (Leetcode:162)
Problem Statement
A peak element is an element that is strictly greater than its neighbors.
Given a 0-indexed integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.
You may imagine that nums[-1] = nums[n] = -∞. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in O(log n) time.
Example 1:
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.
Example 2:
Input: nums = [1,2,1,3,5,6,4]
Output: 5
Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
Constraints:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1nums[i] != nums[i + 1]for all validi.
6. Predicate / Boolean Function
Problem 1: First Bad Version (Leetcode:278)
Problem Statement
You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API bool isBadVersion(version) which returns whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
Example 1:
Input: n = 5, bad = 4
Output: 4
Explanation:
call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true
Then 4 is the first bad version.
Example 2:
Input: n = 1, bad = 1
Output: 1
Constraints:
1 <= bad <= n <= 231 - 1
Problem 2: Find Peak Element (Leetcode:162)
Problem Statement
A peak element is an element that is strictly greater than its neighbors.
Given a 0-indexed integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.
You may imagine that nums[-1] = nums[n] = -∞. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in O(log n) time.
Example 1:
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.
Example 2:
Input: nums = [1,2,1,3,5,6,4]
Output: 5
Explanation: Your function can return either index number 1 where the peak element is 2, or index number 5 where the peak element is 6.
Constraints:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1nums[i] != nums[i + 1]for all validi.
Problem 3: Sqrt(x) (Leetcode:69)
Problem Statement
Given a non-negative integer x, return the square root of x rounded down to the nearest integer. The returned integer should be non-negative as well.
You must not use any built-in exponent function or operator.
- For example, do not use
pow(x, 0.5)in c++ orx ** 0.5in python.
Example 1:
Input: x = 4
Output: 2
Explanation: The square root of 4 is 2, so we return 2.
Example 2:
Input: x = 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since we round it down to the nearest integer, 2 is returned.
Constraints:
0 <= x <= 231 - 1
7. 2D Binary Search
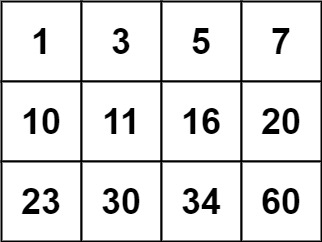
Problem 1: Search a 2D Matrix (Leetcode:74)
Problem Statement
You are given an m x n integer matrix matrix with the following two properties:
- Each row is sorted in non-decreasing order.
- The first integer of each row is greater than the last integer of the previous row.
Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
Example 1:
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
Example 2:
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
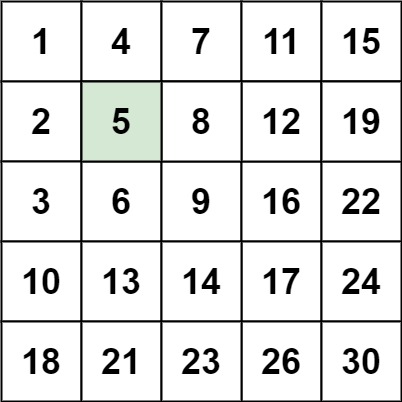
Problem 2: Search a 2D Matrix II (Leetcode:240)
Problem Statement
Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true
Example 2:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109