11. Divide and Conquer
1. Basic Divide and Conquer (Recursive Decomposition)
Classic problems that break a problem into smaller subproblems, solve recursively, then combine.
Problem 1: Merge Sort (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 2: Quick Sort (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 3: Maximum Subarray Sum - Divide and Conquer Approach (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 4: Count Inversions in an Array (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 5: Closest Pair of Points (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 6: Integer Multiplication - Karatsuba / Toom-Cook (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 7: Search in Rotated Sorted Array (Leetcode:33)
Problem Statement
There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is possibly left rotated at an unknown index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be left rotated by 3 indices and become [4,5,6,7,0,1,2].
Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
Example 3:
Input: nums = [1], target = 0
Output: -1
Constraints:
1 <= nums.length <= 5000-104 <= nums[i] <= 104- All values of
numsare unique.numsis an ascending array that is possibly rotated.-104 <= target <= 104
2. Binary Search on Answer / Search Space
Problems where binary search is applied not on array indices but on the value or answer space.
Problem 1: Allocate Minimum Number of Pages (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 2: Koko Eating Bananas (Leetcode:875)
Problem Statement
Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.
Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return the minimum integer k such that she can eat all the bananas within h hours.
Example 1:
Input: piles = [3,6,7,11], h = 8
Output: 4
Example 2:
Input: piles = [30,11,23,4,20], h = 5
Output: 30
Example 3:
Input: piles = [30,11,23,4,20], h = 6
Output: 23
Constraints:
1 <= piles.length <= 104piles.length <= h <= 1091 <= piles[i] <= 109
Problem 3: Split Array Largest Sum (Leetcode:410)
Problem Statement
Given an integer array nums and an integer k, split nums into k non-empty subarrays such that the largest sum of any subarray is minimized.
Return the minimized largest sum of the split.
A subarray is a contiguous part of the array.
Example 1:
Input: nums = [7,2,5,10,8], k = 2
Output: 18
Explanation: There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8], where the largest sum among the two subarrays is only 18.
Example 2:
Input: nums = [1,2,3,4,5], k = 2
Output: 9
Explanation: There are four ways to split nums into two subarrays.
The best way is to split it into [1,2,3] and [4,5], where the largest sum among the two subarrays is only 9.
Constraints:
1 <= nums.length <= 10000 <= nums[i] <= 1061 <= k <= min(50, nums.length)
Problem 4: Median of Two Sorted Arrays (Leetcode:4)
Problem Statement
Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.
The overall run time complexity should be O(log (m+n)).
Example 1:
Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.
Example 2:
Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
Constraints:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
Problem 5: Aggressive Cows (SPOJ - AGGRCOW)
Problem Statement
Example 1:
Example 2:
Constraints:
3. Divide and Conquer on Data Structures
Divide and conquer applied to trees, arrays, strings, or other data structures for complex queries.
Problem 1: Lowest Common Ancestor in a Binary Tree (Leetcode:236)
Problem Statement
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 105].-109 <= Node.val <= 109- All
Node.valare unique.p != qpandqwill exist in the tree.
Problem 2: Count Nodes in Complete Binary Tree (Leetcode:222)
Problem Statement
Given the root of a complete binary tree, return the number of the nodes in the tree.
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
Design an algorithm that runs in less than O(n) time complexity.
Example 1:
Input: root = [1,2,3,4,5,6]
Output: 6
Example 2:
Input: root = []
Output: 0
Example 3:
Input: root = [1]
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[0, 5 * 104].0 <= Node.val <= 5 * 104- The tree is guaranteed to be complete.
Problem 3: Segment Tree Construction (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 4: Maximum Depth of Binary Tree (Leetcode:104)
Problem Statement
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
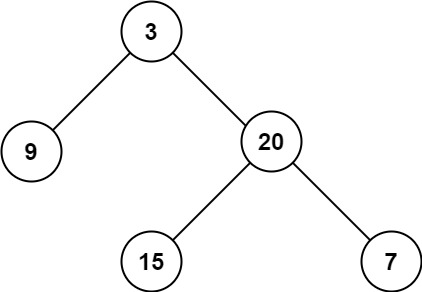
Example 1:
Input: root = [3,9,20,null,null,15,7]
Output: 3
Example 2:
Input: root = [1,null,2]
Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 104].-100 <= Node.val <= 100
Problem 5: Binary Lifting for Ancestor Queries (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
4. Master Theorem / Recurrence Relation
Problems focusing on solving recurrences or analyzing time complexity of divide and conquer algorithms.
Problem 1: Analyze Merge Sort Time Complexity (Conceptual)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 2: Solve Recurrence T(n) = 2T(n/2) + O(n) (Conceptual)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 3: Strassen’s Matrix Multiplication (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 4: Karatsuba Multiplication (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
5. Divide and Conquer with Memoization (Dynamic Programming)
Combining divide and conquer with caching to avoid repeated computations.
Problem 1: Fibonacci Number with Memoization (Leetcode:509)
Problem Statement
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given n, calculate F(n).
Example 1:
Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:
Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Example 3:
Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
Constraints:
0 <= n <= 30
Problem 2: Unique Binary Search Trees (Leetcode:96)
Problem Statement
Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.
Example 1:
Input: n = 3
Output: 5
Example 2:
Input: n = 1
Output: 1
Constraints:
1 <= n <= 19
Problem 3: Palindrome Partitioning (Leetcode:131)
Problem Statement
Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.
Example 1:
Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]
Example 2:
Input: s = "a"
Output: [["a"]]
Constraints:
1 <= s.length <= 16scontains only lowercase English letters.
Problem 4: Matrix Chain Multiplication (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 5: Word Break (Leetcode:139)
Problem Statement
Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.
Note that the same word in the dictionary may be reused multiple times in the segmentation.
Example 1:
Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".
Example 2:
Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.
Example 3:
Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false
Constraints:
1 <= s.length <= 3001 <= wordDict.length <= 10001 <= wordDict[i].length <= 20sandwordDict[i]consist of only lowercase English letters.- All the strings of
wordDictare unique.
Problem 6: Edit Distance (Leetcode:72)
Problem Statement
Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.
You have the following three operations permitted on a word:
- Insert a character
- Delete a character
- Replace a character
Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
Constraints:
0 <= word1.length, word2.length <= 500word1andword2consist of lowercase English letters.