12. Backtracking
1. Basic Backtracking (Permutation, Combination, Subset Generation)
Classic problems generating permutations, combinations, or subsets via recursion and backtracking.
Problem 1: Permutations (Leetcode:46)
Problem Statement
Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.
Example 1:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Example 2:
Input: nums = [0,1]
Output: [[0,1],[1,0]]
Example 3:
Input: nums = [1]
Output: [[1]]
Constraints:
1 <= nums.length <= 6-10 <= nums[i] <= 10- All the integers of
numsare unique.
Problem 2: Combinations (Leetcode:77)
Problem Statement
Given two integers n and k, return all possible combinations of k numbers chosen from the range [1, n].
You may return the answer in any order.
Example 1:
Input: n = 4, k = 2
Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Explanation: There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., [1,2] and [2,1] are considered to be the same combination.
Example 2:
Input: n = 1, k = 1
Output: [[1]]
Explanation: There is 1 choose 1 = 1 total combination.
Constraints:
1 <= n <= 201 <= k <= n
Problem 3: Subsets (Leetcode:78)
Problem Statement
Given an integer array nums of unique elements, return all possible subsets (the power set).
The solution set must not contain duplicate subsets. Return the solution in any order.
Example 1:
Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
Example 2:
Input: nums = [0]
Output: [[],[0]]
Constraints:
1 <= nums.length <= 10-10 <= nums[i] <= 10- All the numbers of
numsare unique.
Problem 4: Letter Case Permutation (Leetcode:784)
Problem Statement
Given a string s, you can transform every letter individually to be lowercase or uppercase to create another string.
Return a list of all possible strings we could create. Return the output in any order.
Example 1:
Input: s = "a1b2"
Output: ["a1b2","a1B2","A1b2","A1B2"]
Example 2:
Input: s = "3z4"
Output: ["3z4","3Z4"]
Constraints:
1 <= s.length <= 12sconsists of lowercase English letters, uppercase English letters, and digits.
2. Backtracking with Constraints (N-Queens, Sudoku, Graph Coloring)
Backtracking with added constraints to prune search space.
Problem 1: N-Queens (Leetcode:51)
Problem Statement
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1
Output: [["Q"]]
Constraints:
1 <= n <= 9
Problem 2: Sudoku Solver (Leetcode:37)
Problem Statement
Write a program to solve a Sudoku puzzle by filling the empty cells.
A sudoku solution must satisfy all of the following rules:
- Each of the digits
1-9must occur exactly once in each row. - Each of the digits
1-9must occur exactly once in each column. - Each of the digits
1-9must occur exactly once in each of the 93x3sub-boxes of the grid.
The '.' character indicates empty cells.
Example 1:
Input: board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
Explanation: The input board is shown above and the only valid solution is shown below:
Constraints:
board.length == 9board[i].length == 9board[i][j]is a digit or'.'.- It is guaranteed that the input board has only one solution.
Problem 3: Graph Coloring Problem (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
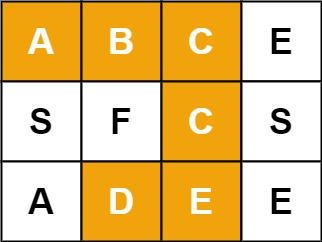
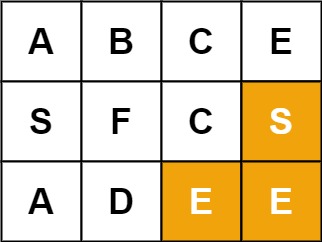
Problem 4: Word Search (Leetcode:79)
Problem Statement
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Example 2:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true
Example 3:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false
Constraints:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15boardandwordconsists of only lowercase and uppercase English letters.
Follow up: Could you use search pruning to make your solution faster with a larger board?
3. Backtracking with Combinatorial Optimization (Subset Sum, Partition, Palindrome Partitioning)
Problems where backtracking is used to explore subsets or partitions optimizing certain conditions.
Problem 1: Partition Equal Subset Sum (Leetcode:416)
Problem Statement
Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.
Example 1:
Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
Example 2:
Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.
Constraints:
1 <= nums.length <= 2001 <= nums[i] <= 100
Problem 2: Combination Sum (Leetcode:39)
Problem Statement
Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.
The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
The test cases are generated such that the number of unique combinations that sum up to target is less than 150 combinations for the given input.
Example 1:
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.
Example 2:
Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]
Example 3:
Input: candidates = [2], target = 1
Output: []
Constraints:
1 <= candidates.length <= 302 <= candidates[i] <= 40- All elements of
candidatesare distinct.1 <= target <= 40
Problem 3: Palindrome Partitioning (Leetcode:131)
Problem Statement
Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.
Example 1:
Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]
Example 2:
Input: s = "a"
Output: [["a"]]
Constraints:
1 <= s.length <= 16scontains only lowercase English letters.
Problem 4: Subset Sum (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
4. Backtracking with Pruning and Early Stopping
Optimizing backtracking using pruning techniques like sorting, bounding, or memoization.
Problem 1: N-Queens with Pruning (Leetcode:51)
Problem Statement
The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.
Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order**.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.
Example 1:
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above
Example 2:
Input: n = 1
Output: [["Q"]]
Constraints:
1 <= n <= 9
Problem 2: Word Search with Pruning (Leetcode:79)
Problem Statement
Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Example 2:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true
Example 3:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false
Constraints:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15boardandwordconsists of only lowercase and uppercase English letters.
Follow up: Could you use search pruning to make your solution faster with a larger board?
Problem 3: Combination Sum II (avoid duplicates) (Leetcode:40)
Problem Statement
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
Each number in candidates may only be used once in the combination.
Note: The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [10,1,2,7,6,1,5], target = 8
Output:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5
Output:
[
[1,2,2],
[5]
]
Constraints:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
5. Backtracking on Grids / Maze Problems
Exploring paths or all possible moves on grids, mazes, or board games.
Problem 1: Rat in a Maze (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 2: Knight’s Tour Problem (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 3: Number of Islands (DFS + Backtracking variant) (Leetcode:200)
Problem Statement
Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1
Example 2:
Input: grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
Output: 3
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]is'0'or'1'.
6. Backtracking with State Restoration (Sudoku, Permutation with Duplicates)
Backtracking problems where careful state restoration is key for correctness and efficiency.
Problem 1: Permutations II (handling duplicates) (Leetcode:47)
Problem Statement
Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.
Example 1:
Input: nums = [1,1,2]
Output:
[[1,1,2],
[1,2,1],
[2,1,1]]
Example 2:
Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
Constraints:
1 <= nums.length <= 8-10 <= nums[i] <= 10
Problem 2: Combination Sum II (Leetcode:40)
Problem Statement
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
Each number in candidates may only be used once in the combination.
Note: The solution set must not contain duplicate combinations.
Example 1:
Input: candidates = [10,1,2,7,6,1,5], target = 8
Output:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5
Output:
[
[1,2,2],
[5]
]
Constraints:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
Problem 3: Restore IP Addresses (Leetcode:93)
Problem Statement
valid IP address consists of exactly four integers separated by single dots. Each integer is between 0 and 255 (inclusive) and cannot have leading zeros.
- For example,
"0.1.2.201"and"192.168.1.1"are valid IP addresses, but"0.011.255.245","192.168.1.312"and"192.168@1.1"are invalid IP addresses.
Given a string s containing only digits, return all possible valid IP addresses that can be formed by inserting dots into s. You are not allowed to reorder or remove any digits in s. You may return the valid IP addresses in any order.
Example 1:
Input: s = "25525511135"
Output: ["255.255.11.135","255.255.111.35"]
Example 2:
Input: s = "0000"
Output: ["0.0.0.0"]
Example 3:
Input: s = "101023"
Output: ["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
Constraints:
1 <= s.length <= 20sconsists of digits only.
Code and Explaination
7. Backtracking with Bitmasking (Subset States, TSP)
Using bitmasking to efficiently represent subsets or states during backtracking.
Problem 1: Traveling Salesman Problem (TSP) (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 2: Count number of ways/subsets using bitmasking ([Various competitive programming resources])
Problem Statement
Example 1:
Example 2:
Constraints:
8. Backtracking with Graph Traversal (Paths and Cycles)
Backtracking on graphs to find all paths, cycles, or solve Hamiltonian problems.
Problem 1: Find All Paths from Source to Destination (Leetcode:797)
Problem Statement
Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
Example 1:
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.
Example 2:
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Constraints:
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i(i.e., there will be no self-loops).- All the elements of
graph[i]are unique.- The input graph is guaranteed to be a DAG.
Problem 2: Hamiltonian Path Problem (GeeksforGeeks)
Problem Statement
Example 1:
Example 2:
Constraints:
Problem 3: Word Ladder / Word Transformation Variants (Leetcode:127)
Problem Statement
A transformation sequence from word beginWord to word endWord using a dictionary wordList is a sequence of words beginWord -> s1 -> s2 -> ... -> sk such that:
- Every adjacent pair of words differs by a single letter.
- Every
sifor1 <= i <= kis inwordList. Note thatbeginWorddoes not need to be inwordList. sk == endWord
Given two words, beginWord and endWord, and a dictionary wordList, return the number of words in the shortest transformation sequence from beginWord to endWord, or 0 if no such sequence exists.
Example 1:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: One shortest transformation sequence is "hit" -> "hot" -> "dot" -> "dog" -> cog", which is 5 words long.
Example 2:
Input: beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore there is no valid transformation sequence.
Constraints:
1 <= beginWord.length <= 10endWord.length == beginWord.length1 <= wordList.length <= 5000wordList[i].length == beginWord.lengthbeginWord,endWord, andwordList[i]consist of lowercase English letters.beginWord != endWord- All the words in
wordListare unique.
9. Backtracking with Memoization / Top-Down DP
Combining backtracking with caching to avoid repeated computations in overlapping subproblems.
Problem 1: Decode Ways (Leetcode:91)
Problem Statement
You have intercepted a secret message encoded as a string of numbers. The message is decoded via the following mapping:
"1" -> 'A'
"2" -> 'B'
...
"25" -> 'Y'
"26" -> 'Z'
However, while decoding the message, you realize that there are many different ways you can decode the message because some codes are contained in other codes ("2" and "5" vs "25").
For example, "11106" can be decoded into:
"AAJF"with the grouping(1, 1, 10, 6)"KJF"with the grouping(11, 10, 6)- The grouping
(1, 11, 06)is invalid because"06"is not a valid code (only"6"is valid).
Note: there may be strings that are impossible to decode.
Given a string s containing only digits, return the number of ways to decode it. If the entire string cannot be decoded in any valid way, return 0.
The test cases are generated so that the answer fits in a 32-bit integer.
Example 1:
Input: s = "12"
Output: 2
Explanation:
"12" could be decoded as "AB" (1 2) or "L" (12).
Example 2:
Input: s = "226"
Output: 3
Explanation:
"226" could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).
Example 3:
Input: s = "06"
Output: 0
Explanation:
"06" cannot be mapped to "F" because of the leading zero ("6" is different from "06"). In this case, the string is not a valid encoding, so return 0.
Constraints:
1 <= s.length <= 100scontains only digits and may contain leading zero(s).
Problem 2: Wildcard Matching (Leetcode:44)
Problem Statement
Given an input string (s) and a pattern (p), implement wildcard pattern matching with support for '?' and '*' where:
'?'Matches any single character.'*'Matches any sequence of characters (including the empty sequence).
The matching should cover the entire input string (not partial).
Example 1:
Input: s = "aa", p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".
Example 2:
Input: s = "aa", p = ""
Output: true
Explanation: '' matches any sequence.
Example 3:
Input: s = "cb", p = "?a"
Output: false
Explanation: '?' matches 'c', but the second letter is 'a', which does not match 'b'.
Constraints:
0 <= s.length, p.length <= 2000scontains only lowercase English letters.pcontains only lowercase English letters,'?'or'*'.