18. Segment Tree

Theory

Problems

Problem 1: Range Sum Query - Mutable (Leetcode:307)

Problem Statement

Given an integer array nums, handle multiple queries of the following types:

Update the value of an element in nums.
Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Implement the NumArray class:

NumArray(int[] nums) Initializes the object with the integer array nums.
void update(int index, int val) Updates the value of nums[index] to be val.
int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

Example 1:

Input
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
Output
[null, 9, null, 8]

Explanation
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2); // nums = [1, 2, 5]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8

Constraints:

1 <= nums.length <= 3 * 104

-100 <= nums[i] <= 100

0 <= index < nums.length

-100 <= val <= 100

0 <= left <= right < nums.length

At most 3 * 104 calls will be made to update and sumRange.

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach

Problem 2: Range Sum Query - Immutable (Leetcode:303)

Problem Statement

Given an integer array nums, handle multiple queries of the following type:

Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Implement the NumArray class:

NumArray(int[] nums) Initializes the object with the integer array nums.
int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive (i.e. nums[left] + nums[left + 1] + ... + nums[right]).

Example 1:

Input
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
Output
[null, 1, -1, -3]

Explanation
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return (-2) + 0 + 3 = 1
numArray.sumRange(2, 5); // return 3 + (-5) + 2 + (-1) = -1
numArray.sumRange(0, 5); // return (-2) + 0 + 3 + (-5) + 2 + (-1) = -3

Constraints:

1 <= nums.length <= 104

-105 <= nums[i] <= 105

0 <= left <= right < nums.length

At most 104 calls will be made to sumRange.

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach

Problem 3: Count of Smaller Numbers After Self (Leetcode:315)

Problem Statement

Given an integer array nums, return an integer array counts where counts[i] is the number of smaller elements to the right of nums[i].

Example 1:

Input: nums = [5,2,6,1]
Output: [2,1,1,0]
Explanation:
To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.

Example 2:

Input: nums = [-1]
Output: [0]

Example 3:

Input: nums = [-1,-1]
Output: [0,0]

Constraints:

1 <= nums.length <= 105

-104 <= nums[i] <= 104

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach

Problem 4: The Skyline Problem (Leetcode:218)

Problem Statement

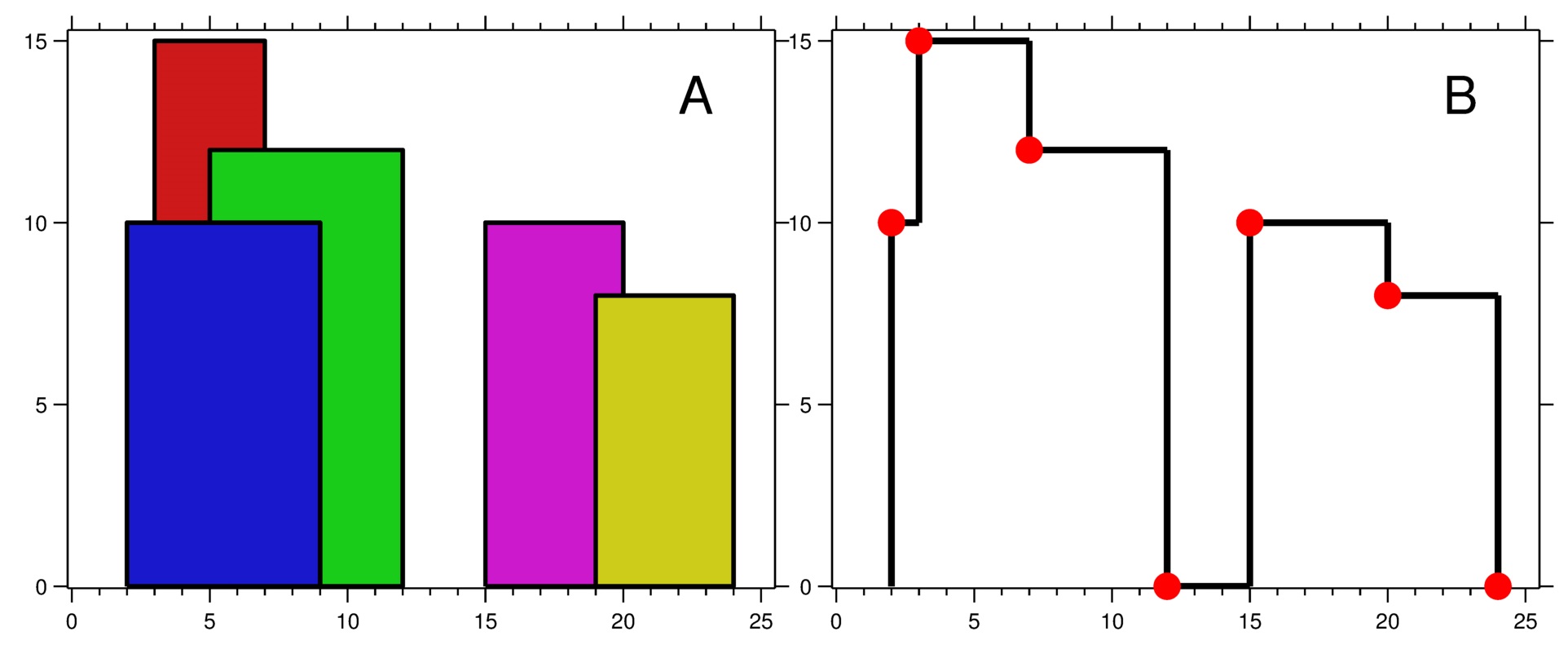
A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

lefti is the x coordinate of the left edge of the ith building.
righti is the x coordinate of the right edge of the ith building.
heighti is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:

Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:

Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints:

1 <= buildings.length <= 104

0 <= lefti < righti <= 231 - 1

1 <= heighti <= 231 - 1

buildings is sorted by lefti in non-decreasing order.

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach

Problem 5: Queue Reconstruction by Height (Leetcode:406)

Problem Statement

You are given an array of people, people, which are the attributes of some people in a queue (not necessarily in order). Each people[i] = [hi, ki] represents the ith person of height hi with exactly ki other people in front who have a height greater than or equal to hi.

Reconstruct and return the queue that is represented by the input array people. The returned queue should be formatted as an array queue, where queue[j] = [hj, kj] is the attributes of the jth person in the queue (queue[0] is the person at the front of the queue).

Example 1:

Input: people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
Output: [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
Explanation:
Person 0 has height 5 with no other people taller or the same height in front.
Person 1 has height 7 with no other people taller or the same height in front.
Person 2 has height 5 with two persons taller or the same height in front, which is person 0 and 1.
Person 3 has height 6 with one person taller or the same height in front, which is person 1.
Person 4 has height 4 with four people taller or the same height in front, which are people 0, 1, 2, and 3.
Person 5 has height 7 with one person taller or the same height in front, which is person 1.
Hence [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] is the reconstructed queue.

Example 2:

Input: people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
Output: [[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

Constraints:

1 <= people.length <= 2000

0 <= hi <= 106

0 <= ki < people.length

It is guaranteed that the queue can be reconstructed.

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach

Problem 6: Rectangle Area II (Leetcode:850)

Problem Statement

You are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.

Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.

Return the total area. Since the answer may be too large, return it modulo** 109 + 7.

Example 1:

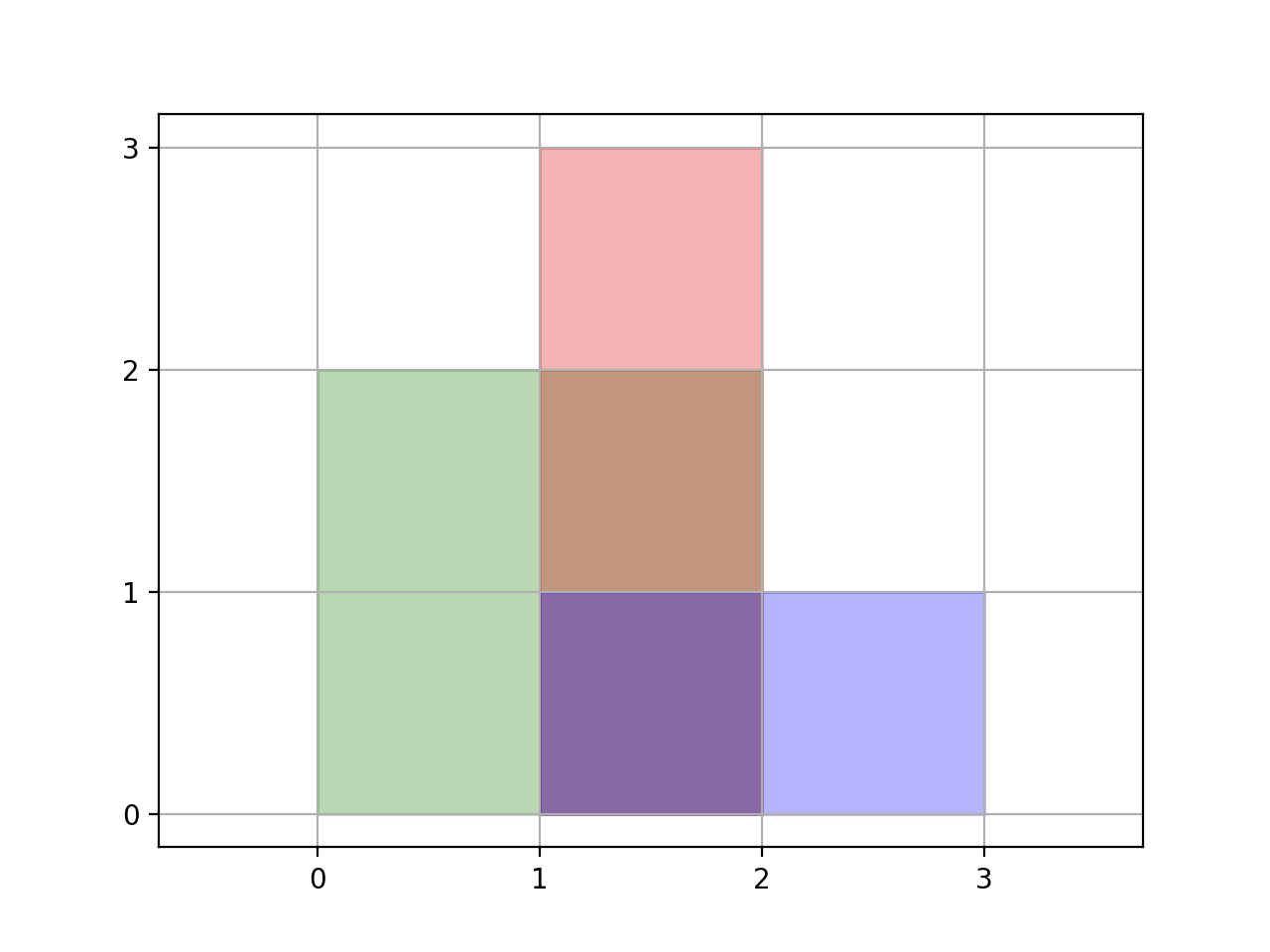
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: A total area of 6 is covered by all three rectangles, as illustrated in the picture.
From (1,1) to (2,2), the green and red rectangles overlap.
From (1,0) to (2,3), all three rectangles overlap.

Example 2:

Input: rectangles = [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 1018 modulo (109 + 7), which is 49.

Constraints:

1 <= rectangles.length <= 200

rectanges[i].length == 4

0 <= xi1, yi1, xi2, yi2 <= 109

xi1 <= xi2

yi1 <= yi2

All rectangles have non zero area.

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach

Problem 7: Fancy Sequence (Leetcode:1622)

Problem Statement

Write an API that generates fancy sequences using the append, addAll, and multAll operations.

Implement the Fancy class:

Fancy() Initializes the object with an empty sequence.
void append(val) Appends an integer val to the end of the sequence.
void addAll(inc) Increments all existing values in the sequence by an integer inc.
void multAll(m) Multiplies all existing values in the sequence by an integer m.
int getIndex(idx) Gets the current value at index idx (0-indexed) of the sequence modulo 109 + 7. If the index is greater or equal than the length of the sequence, return -1.

Example 1:

Input
["Fancy", "append", "addAll", "append", "multAll", "getIndex", "addAll", "append", "multAll", "getIndex", "getIndex", "getIndex"]
[[], [2], [3], [7], [2], [0], [3], [10], [2], [0], [1], [2]]
Output
[null, null, null, null, null, 10, null, null, null, 26, 34, 20]

Explanation
Fancy fancy = new Fancy();
fancy.append(2); // fancy sequence: [2]
fancy.addAll(3); // fancy sequence: [2+3] -> [5]
fancy.append(7); // fancy sequence: [5, 7]
fancy.multAll(2); // fancy sequence: [52, 72] -> [10, 14]
fancy.getIndex(0); // return 10
fancy.addAll(3); // fancy sequence: [10+3, 14+3] -> [13, 17]
fancy.append(10); // fancy sequence: [13, 17, 10]
fancy.multAll(2); // fancy sequence: [132, 172, 10*2] -> [26, 34, 20]
fancy.getIndex(0); // return 26
fancy.getIndex(1); // return 34
fancy.getIndex(2); // return 20

Constraints:

1 <= val, inc, m <= 100

0 <= idx <= 105

At most 105 calls total will be made to append, addAll, multAll, and getIndex.

Code and Explaination

Approach 1Approach 2

Explaination:
This is first approach

Explaination:
This is second approach